Størrelsestype med Lucas Sequences
Forholdet mellom tekst og resten av en side er et av hovedtrekkene til ethvert design.
Rytme, vekt og tone er alle kompromittert uten riktig skalertype. Valg av tekststørrelser er imidlertid ofte en omhyggelig og frustrerende opplevelse, uten standardisert utgangspunkt for å informere oss.
Som et resultat finner vi ofte webdesignere som faller tilbake på standardvalgene som presenteres av applikasjoner - 8pt, 10pt, 12pt, 14pt, 18pt - for å ha en bedre løsning.
Den bedre løsningen er å sette type størrelser ikke av individuelle innfall, men ifølge et forhåndsbestemt system; et system som er enkelt å bruke, praktisk å implementere på nettet og viktigst, fleksibelt nok til å gi designere et komplett spekter av uttrykk. Cue: Lucas-sekvensen.
Lucas sekvenser
Fibonacci-sekvensen - først registrert i vest i det 13. århundre av Leonardo Fibonacci - er følgende sett med heltall (hele tall):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ... ad infinitum
Sekvensen ble oppkalt etter Fibonacci av den fremtredende franske matematikeren François Édouard Lucas, som produserte en lignende sekvens som han refererte til som Lucas Numbers:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 ... ad infinitum
Fibonacci Sequence og Lucas Numbers er begge spesifikke variasjoner av den generiske Lucas Sequence.
Lucas Sekvenser og heltallssekvenser generelt har vært gjenstand for en levetid for studier for mange dyktige matematikere, så vi skal oppsummere konseptet som følger:
- Ethvert gitt tall i sekvensen er summen av de to foregående tallene som beskrevet i denne formelen: n = n-1 + n-2
- De to første tallene i sekvensen, kjent som frønumre, velges vilkårlig.
Hvorfor bruke en Lucas sekvens for å sette type?
Lucas-sekvenser, spesielt i form av Fibonacci-sekvensen, har et nært forhold til Golden Ratio, som gjentas gjennom naturen i skall, spindelbaner, skyformasjoner og mange andre naturlige underverk. Det er sterke bevis for at noe vi finner visuelt tiltalende, skyldes at formens forhold til det gyldne forholdet.
Enda viktigere, Lucas Sequences gir oss et skalerbart rammeverk for å sette type som er både grasiøs og rytmisk.
Bestemme vårt første frø nummer
Det er mye debatt om riktig tekststørrelse for et nettsted. 12px er fortsatt den vanligste, men det er ikke uvanlig å se alt fra 10px til 16px. Dette er vesentlig født av mangel på forståelse av hvilke skriftmålinger som egentlig betyr. Merkelig, for de som er vant til standardisering - eller i det minste ambisjoner om standardisering - finnes det ingen standardmål i type design; to forskjellige type designere, tegner nøyaktig samme design i skriftproduksjonsprogramvare, sannsynligvis vil tegne den i forskjellige størrelser. Variasjonen mellom forskjellige skrifttyper er ikke overraskende altfor vanlig.

Svaret på hvor du skal begynne er infuriatingly simple; Vår standard tekststørrelse vil være 1em, noe som betyr at vårt første frønummer vil være 1.
Det er en rekke viktige fordeler ved å bruke 1em som utgangspunkt: Som en relativ måleenhet er en em velegnet til lydhør design; ved å bruke ems og multipler av ems kan vi endre størrelsen på hele vårt system ved å endre basestørrelsesstørrelsen; til slutt er det en fin konseptuell passform med vår Lucas-sekvens og vil tjene til å minne oss om den nøyaktige heltallssekvensen hvis vi trenger å gå tilbake til designet senere.
Det er ingenting iboende feil med å bruke prosentandeler i stedet for ems, eller til og med piksler eller poeng, men em er mer enn sannsynlig fremtiden for webdesign, så vi kan like godt bli vant til det.
Bestemme vårt andre frø nummer
Det er mange strategier som er åpne for oss for å bestemme vårt andre frønummer. Noen designere har en bestemt preferanse og vil velge 1.2em eller lignende. Andre designere, som liker mystikken i Golden Ratio, kan gjerne bruke 1.618em.
En mer praktisk løsning er å bestemme det andre frønummeret ved hjelp av linjehøyden i kroppsteksten. Men fordi linjestørrelsen vanligvis dikteres av lengden på linjen og linjelengden bestemmes av et rutenett, er det mer egnet til å skrive ut eller ikke-responsivt webdesign. Fordi vi ser fremover, og fremtiden er responsiv, vil den ikke fungere for oss.
Det vi er igjen med, delvis av en elimineringsprosess og delvis på grunn av dets hensiktsmessighet, er typens x-høyde. Eller nærmere bestemt forholdet mellom x-høyden og resten av glyphen.
Et kjennetegn ved god design er repetisjonen av nøkkelelementer, og å bære proporsjonene av typen gjennom til siden som helhet er en flott mulighet til å begge anerkjenne typedesigners arbeid og bøye vårt design med noen av tegnets karakter.
Finne vår x-høyde
For å finne x-høyden på fonten din, må vi åpne noe som Photoshop eller Illustrator, og legge til litt tekst som inkluderer en stigende (f.eks. D) og bokstaven 'x'. Hvis du bruker en bitmap-editor som Photoshop, må du sette teksten så stor som mulig for å sikre at du får et nøyaktig resultat. I disse eksemplene har jeg satt skrift til 500pt for å måle det.
Deretter måler høyden fra oppstigningslinjen til grunnlinjen og høyden fra toppen av x til grunnlinjen.
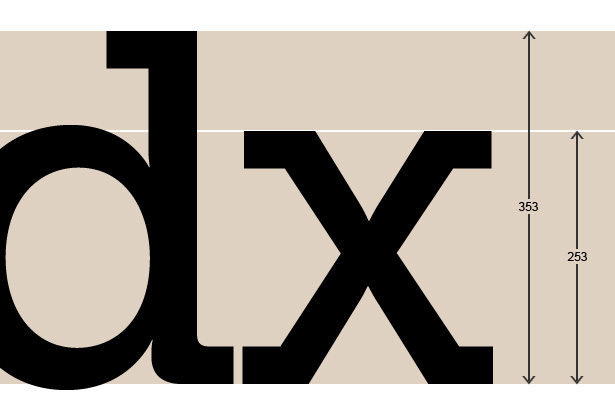
Selvfølgelig, hvis du er heldig nok til å få tilgang til god skrifttypedesign, kan du ganske enkelt åpne fontfilen du vil bruke og lese av x-høyden og oppstigningshøyden.
Del nå x-høyden av stigningshøyden for å finne x-høyden som en prosentandel av hele:
x-høyde / stigende høyde * 100 = andre frø nummer
I tilfelle av skrifttypen i eksemplet (som er Museo Slab) er resultatet:
253/353 = 0,71671388
eller 0,716em
Hvorfor måler vi ikke fra toppen av stigeren til bunnen av nedstigningen? Fordi tegn ikke har en tendens til å ha både en stigende og nedstigende (et sporadisk unntak er bokstaven "f") og følgelig er forholdene i formene som består av skrifttypens utforming basert på forholdet mellom x-høyden og en lengre stamme. Det er mulig å måle nedstigeren i stedet, men som kapphøyde (hovedstadenes høyde) er vanligvis svært nær oppstigeren, er det min preferanse. Hvis du finner deg selv ved hjelp av et skrifttype med en mer dominerende kvalitet - kontrasten i tykkelsen på forskjellige slag, for eksempel - vil du kanskje bruke den verdien i stedet for stigeren til x-høydeforholdet.
Bestemmelsen av hvordan du kommer til ditt andre frønummer er en av de viktigste designbeslutningene du må gjøre, men det er ikke noe å agonisere over; velg et nummer ut av en lue hvis du foretrekker det, og fortsett, de gode greiene er ennå ikke kommet.
Det er verdt å merke seg at hvis du bytter ligningen rundt og deler oppstigningshøyden med x-høyden, vil du ende opp med et tall som er større enn ett. I så fall vil din rekkefølge bli brattere og litt mer dramatisk.
Opprette vår sekvens
Så, vi har våre to frø tall: 1em og 0.716em og vi har formelen n = n-1 + n-2:
1 + 0,716 = 1,716
0,716 + 1,716 = 2,432
1.716 + 2.432 = 4.148
etc.
Hvilket resulterer i følgende rekkefølge:
1, 0,716, 1,716, 2,432, 4,148, 6,58, 10,728, 17,308, 28,036 ... ad infinitum
Designbiten
Så langt har vi plukket oss gjennom noen grunnleggende, men nyttig matematikk, og vi har kommet fram til en sekvens som gir oss en rekke størrelser fra 1em til 28.036em og utover hvis det er nødvendig.
Vi kan nå bruke disse verdiene som våre typestørrelser i rekkefølge for å skape en velproportjonert type ordning:

Du vil merke at vi starter med p satt til 0.716 og h4 satt til 1, til tross for at det ikke er sekvensielt riktig. Årsaken er at når det gjelder hierarki, er h4 viktigere enn p. Vår Lucas-sekvens må ikke diktere hierarki på siden, det dikterer skalaforholdene til forskjellige elementer. Bare innholdet ditt kan diktere hierarkiet .
Fordi vi ikke er begrenset til sammenhengende verdier i vår sekvens og kan velge og velge hvilke heltall vi bruker, oppnår vi alltid rytme og struktur med samme rekkefølge. Selv om vi tar en veldig dramatisk tilnærming:

Nøyaktig samme Lucas-sekvens kan også brukes til å skape en mer reservert, forretningsmessig ordning:

Kjernen i dette systemet er at skalforholdene opprettholdes, hierarkiet er proporsjonalt, men det er en stor mengde variasjon tilgjengelig for designeren. Dette er hvor du må tjene penger: ved å velge størrelsene på skalaen for å lage hierarki og vekt.
fleksibilitet
Typisk er typestørrelsen diktert av mer enn vekt: problemer med tilgjengelighet oppstår hvis vi snakker om et publikum med visuelle vanskeligheter; det rene volumet av innhold kan kaste opp restriksjoner; Vi må kanskje være fleksible - bokstavelig talt - når du designer en væskeoppsett.
Heldigvis håndterer CSS denne situasjonen med letthet. Fordi vi bruker ems for våre størrelser, kan vi sette opp vår type ved hjelp av vår Lucas Sequence og deretter skalere hele, ved å sette en standardstørrelse på kroppsmerket, beholde rytmen til designet vårt, men øke eller redusere de faktiske verdiene.

Legg merke til i dette bildet at p, h2 og h1 størrelsene forblir de samme, alle trukket fra vår sekvens. Det er variasjonen på skriftstørrelsen til kroppstegnet (0.8em til venstre og 1.4em til høyre) som kaskader ned, og skaper radikalt forskjellige resultater.
Endelig
Som avhengig av underliggende matematikk som dette systemet er, er det viktig å erkjenne at design ikke kan reduseres til et sett med ligninger. Denne metoden for dimensjoneringstype gir deg en struktur som du skal arbeide for, og vil hjelpe deg med å skape velproportjonert type ordninger, men det er deg som designer å bruke systemet som et verktøy, ikke som en krykke.
Notene og skalaene i musikk, til og med Jazz, kan reduseres til et sett med likninger som beskriver deres forhold, men det tar noen som John Coltrane å bringe disse relasjonene til liv.